Exploitation of Pairwise Class Distances for Ordinal Classification
J. Sánchez-Monedero (jsanchezm at uco.es) [1], Pedro A. Gutiérrez , Peter Tiño [2], C. Hervás-Martínez.
| [1] | J. Sánchez-Monedero, Pedro A. Gutiérrez and C. Hervás-Martínez are with the Department of Computer Science and Numerical Analysis, University of Córdoba, Campus de Rabanales, C2 building, 14074 - Córdoba, Spain. E-mail: jsanchezm at uco.es, pagutierrez at uco.es, chervas at uco.es. |
| [2] | Peter Tiño is with the School of Computer Science, The University of Birmingham, Birmingham B15 2TT, United Kingdom. E-mail: P.Tino at cs.bham.ac.uk. |
Abstract of the paper
Ordinal classification refers to classification problems in which the classes have a natural order imposed on them because of the nature of the concept studied. Some ordinal classification approaches perform a projection from the input space to 1-dimensional (latent) space that is partitioned into a sequence of intervals (one for each class). Class identity of a novel input pattern is then decided based on the interval its projection falls into. This projection is trained only indirectly as part of the overall model fitting. As with any latent model fitting, direct construction hints one may have about the desired form of the latent model can prove very useful for obtaining high quality models. The key idea of this paper is to construct such a projection model directly, using insights about the class distribution obtained from pairwise distance calculations. The proposed approach is extensively evaluated with eight nominal and ordinal classifiers methods, ten real world ordinal classification datasets, and four different performance measures. The new methodology obtained the best results in average ranking when considering three of the performance metrics, although significant differences are found only for some of the methods. Also, after observing other methods internal behaviour in the latent space, we conclude that the internal projection do not fully reflect the intra-class behaviour of the patterns. Our method is intrinsically simple, intuitive and easily understandable, yet, highly competitive with state-of-the-art approaches to ordinal classification.
Citation details
J. Sanchez-Monedero, P. A. Gutierrez, P. Tino, C. Hervas- Martınez: Exploitation of Pairwise Class Distances for Ordinal Classification.
Neural Computation, Vol. 25, September, 2013, pp. 2450-2485, MIT Press
Bibtex entry
@article{Sanchez-Monedero2013neco,
author = "S{\'a}nchez-Monedero, Javier and Guti{\'e}rrez
and Pedro Antonio and Peter Tino and Herv{\'a}s-Mart{\'i}nez, C{\'e}sar",
journal = "Neural Computation",
year = {2013},
volume = {25},
pages = {2450--2485},
number = {9},
eid = {MIT Press}
}
Please, send bugs and feedback to jsanchezm at uco dot es. All the code is GPLv3 licenced.

1. Introduction
This web page provides supplementary material for the paper entitled Exploitation of Pairwise Class Distances for Ordinal Classification published in Neural Computation (NECO) journal.
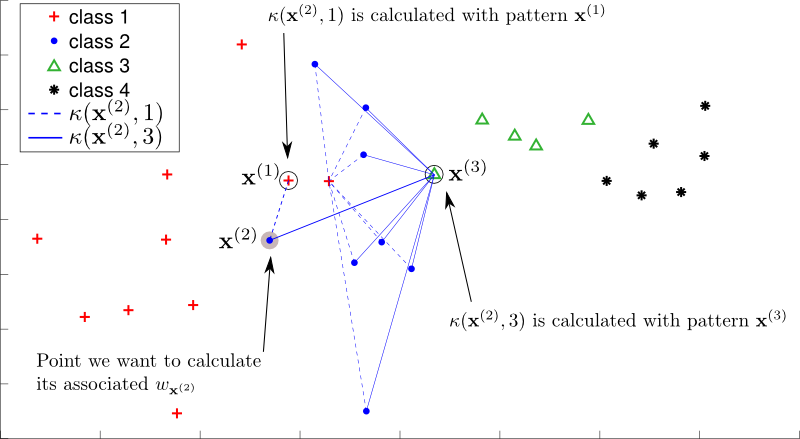
2. Source code
This section provides source code for calculating the Pairwise Class Distance (PCD) projection presented in the paper, and it also presents the Pairwise Class Distance Ordinal Classifier (PCDOC) algorithm. All the source code can be downloaded in a single compressed file together with libSVM 3.0 for Matlab, and with the .mat files for the synthetic datasets: pcdoc-code.zip (this file contains the whole files set needed for executing the algorithm and helper functions). Please, note the source code is not optimized in order to improve the readability.
2.1. Pairwise Class Distance projection and classifier
- Pairwise Class Distance projection: pcdprojection.m
- PCD Ordinal Classifier: PCDOC_classify.m
- Example of training with epsilon-SVR: PCDOC_train.m
- Example of predicting class labels with epsilon-SVR: PCDOC_predict.m
2.2. Synthetic datasets projection analysis
- Synthetic datasets: SyntheticLinearOrder.mat, SyntheticNonLinearOrder.mat
- Projection analysis: pcdprojection_syntheticlinear.m, pcdprojection_syntheticnonlinear.m
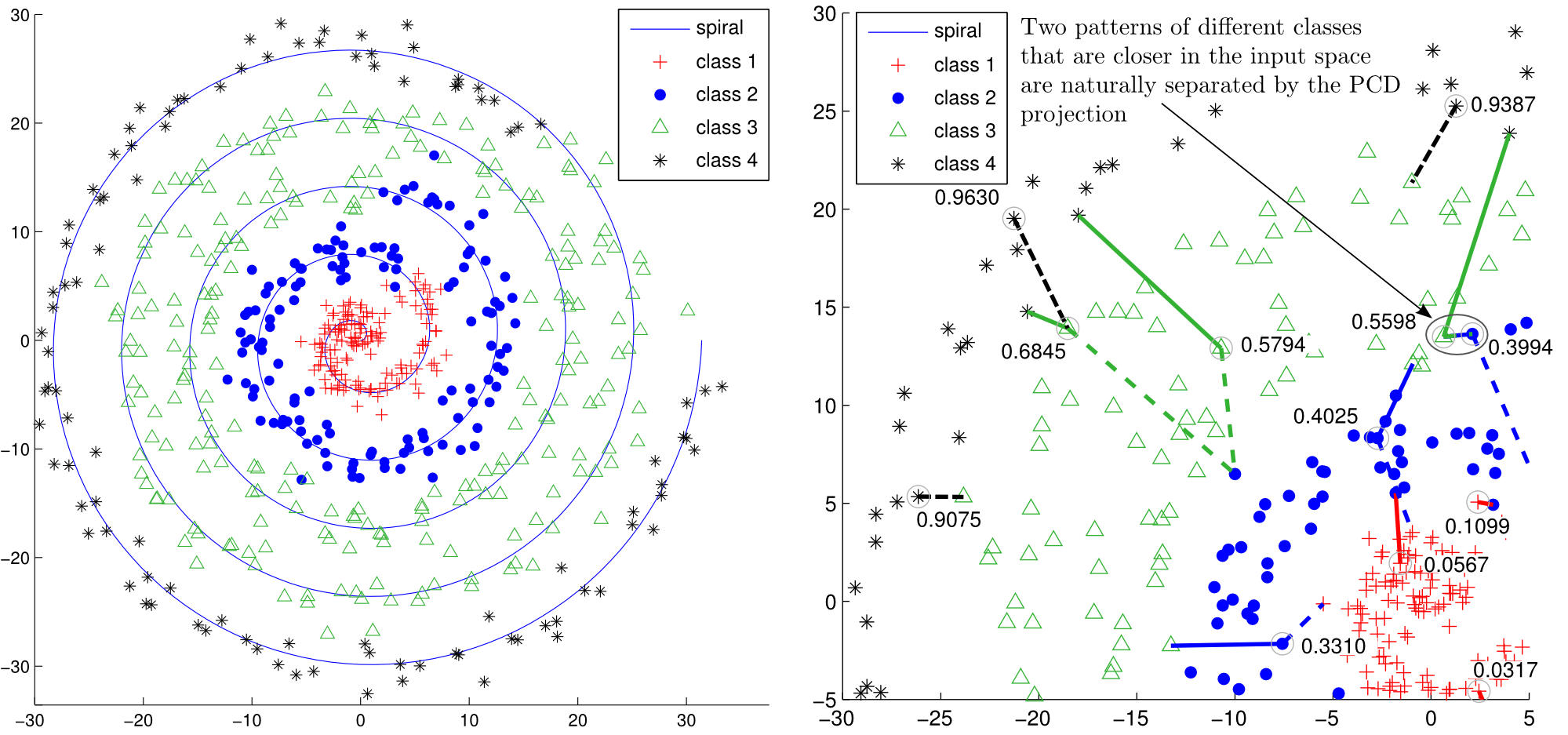
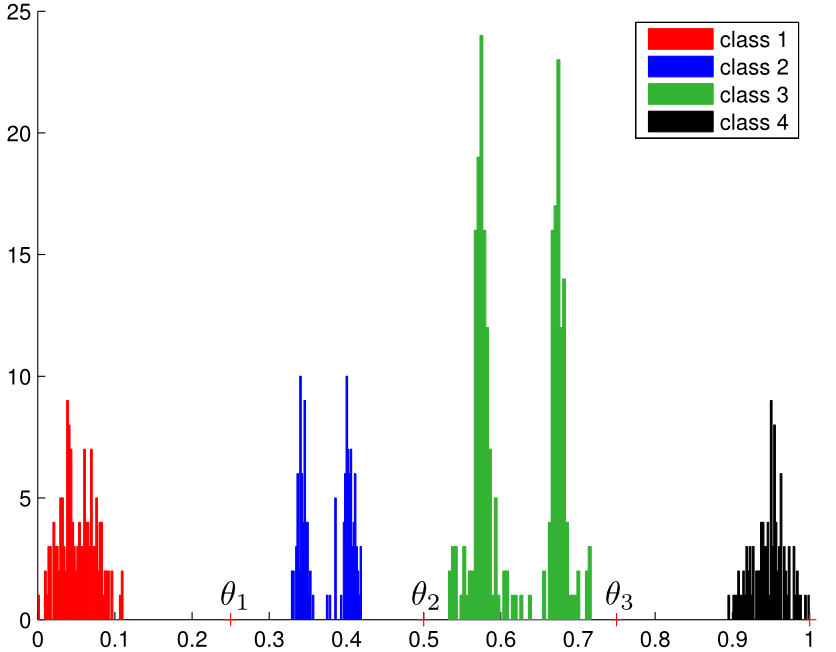
2.3. Auxiliary functions
- PCDOC_preprocess.m: Load, standarize train+test dataset and extract dataset information
- PCDOC_performanceMetrics.m: This function calculates some ordinal classification performance metrics.
2.4. Code execution example
% Execution example of the PCDOC algorithm by using e-SVR as regressor tool
clearvars;
% Add libSVM matlab version. It is compiled for 64bits machines running
% GNU/Linux.
addpath libsvm-mat-3.0-1/
addpath tools/
datasetTrainFile = '../ordinal-classification-datasets/contact-lenses/gpor/train_contact-lenses.0';
datasetTestFile = '../ordinal-classification-datasets/contact-lenses/gpor/test_contact-lenses.0';
% SVR hyperparameters example (must be crossvalided):
hyperparam.k = 0.001;
hyperparam.c = 1000;
hyperparam.e = 0.1000;
% Load and preprocess (standarize) data
dataset = ...
PCDOC_preprocess(datasetTrainFile,datasetTestFile);
% Run PCDOC algorithm
[pcdocModel, TrainPredictedY] = PCDOC_train(dataset.TrainP,dataset.TrainT,dataset.Q, hyperparam);
TestPredictedY = PCDOC_predict(pcdocModel, dataset.TestP, dataset.Q);
% Generate statistics
pmTrain = PCDOC_performanceMetrics(dataset.TrainT, TrainPredictedY);
pmTest = PCDOC_performanceMetrics(dataset.TestT, TestPredictedY);
% Print statistics:
fprintf('\nPerformance metrics:\n');
fprintf('Acc: %f\n', pmTest.acc);
fprintf('MAE: %f\n', pmTest.mae);
fprintf('AMAE: %f\n', pmTest.amae);
fprintf('Kendalls Taub: %f\n', pmTest.kendall);
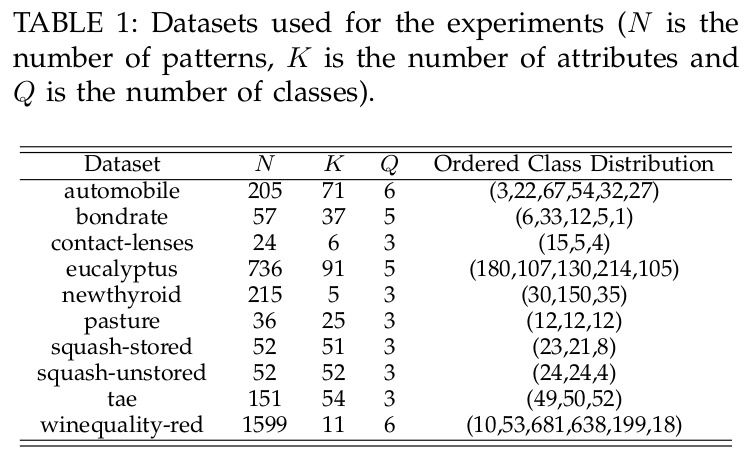
3. Real ordinal classification data sets
This section includes the datasets partitions used for the experiments. All the datasets described in the following above table can be downloaded:
- Ordinal Classificacion datasets (ZIP compressed file)
- Ordinal Classificacion datasets (TAR.GZ compressed file)
Each file contains one folder for each dataset containing the 30-holdout train and generalization (test) partitions. Each partition is in four file formats:
- gpor: GPOR like file format, this is, each pattern is placed in a row with space separated attributes. The last column is the class label in a numeric format. GPOR, SVOR-IN and SVOR-EX algorithms use this format. The proposed method, SVR-PCDOC, uses this file format also. These algorithms assume the dataset files are ordered by class label in ascending order. KDLOR implementation by SVR-PCDOC uses this format also.
- libsvm: libSVM file format.
- weka: Weka file format.
- nnep: JCLEC-NNEP file format (file format description available at Partitions and Source Code section of AYRNA's website)
4. Source code license
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Copyright (C) Javier Sánchez Monedero (jsanchezm at uco dot es) % % This code implements the Pairwise Class Distances (PCD) projection and the % associated PCD Ordinal Classifier (PCDOC). % % The code has been tested with Ubuntu 11.04 x86_64 and Matlab R2009a % % If you use this code, please cite the associated paper % Code updates and citing information: % http://www.uco.es/grupos/ayrna/neco-pairwisedistances % % AYRNA Research group's website: % http://www.uco.es/ayrna % % This program is free software; you can redistribute it and/or % modify it under the terms of the GNU General Public License % as published by the Free Software Foundation; either version 3 % of the License, or (at your option) any later version. % % This program is distributed in the hope that it will be useful, % but WITHOUT ANY WARRANTY; without even the implied warranty of % MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the % GNU General Public License for more details. % % You should have received a copy of the GNU General Public License % along with this program; if not, write to the Free Software % Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA 02110-1301, USA. % Licence available at: http://www.gnu.org/licenses/gpl-3.0.html %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Learning and Artificial Neural Networks research group website
Javier Sánchez-Monedero et. al 2013







