Example-based Procedural Modeling
by Geometric Constraint Solving
Three-dimensional geometric models are used to represent the shape and design of objects in nearly every type of computer graphics application including virtual environments, Computer-Aided Design and Manufacturing, computer gaming, animated movies, and medical simulations. These applications require complex three-dimensional models to be realistic and compelling. The demand for detailed three-dimensional models is large and expanding. However, satisfying the demand for models is difficult. Realistic models often contain very complex and widely varying shapes and styles. Modeling can be tremendously time-consuming.
Modeling is a creative and artistic process. The objects being modeled may not be based upon real objects, but purely on an artist's imagination. Modeling involves many artistic and high-level design decisions. Decisions about the style and purpose of each object must be made to produce compelling models. Even though creative decisions are an integral part of modeling, in practice, users spend more effort on routine and tedious tasks.
Despite extensive work in geometric modeling for over four decades, it remains a labor-intensive and difficult process even with the best available tools. Current modeling tools are notoriously complex. Learning how to use them requires significant training and even when the tools are mastered creating complex models is still difficult. Modeling complex environments such as cities or landscapes requires creating and manipulating a huge number of primitives and can take many hours or days.
Fortunately, there are many reasons to believe that the modeling process can be greatly simplified and automated. Modeling involves many routine and repetitive tasks. Many of the objects in games, movies, and virtual environments contain repetitive and self-similar structures. Self-similarity is common in man-made objects and natural objects, [1]. Self-similarity is often used to simplify and automate the modeling process. Automation is the goal of procedural modeling techniques. In procedural modeling, automatic procedures are used to generate models.
Many procedural modeling techniques, [2], have been developed for automated or semi-automated generation of complex shapes. These include techniques based on shape grammars, scripting languages, L-systems, fractals, or solid texturing. In practice, they are either limited to a specific class of models or require considerable user input or guidance.
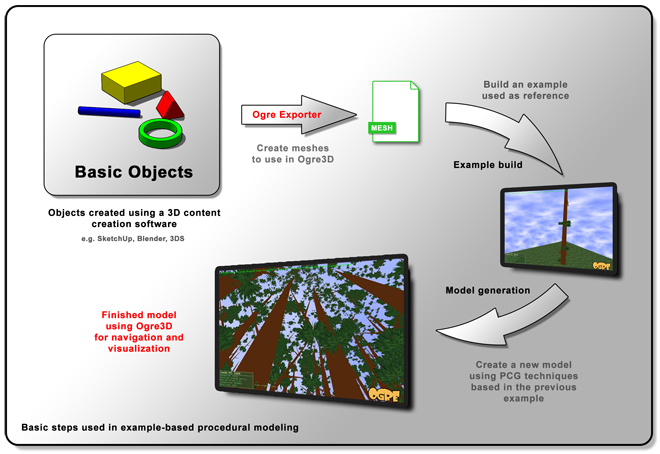
This work explores a new procedural modeling technique that is designed to apply broadly to many classes of objects. It is inspired by recent developments in the texture synthesis literature, [3, 4]. Textures are loosely defined as images containing some type of repeated pattern. The goal of texture synthesis is to create a large texture that resembles an example texture. Texture synthesis is based upon the user specifying what the algorithm should generate by providing an example. Texture synthesis is one of many techniques which use this example-based principle. Example-based techniques are also used for generating high resolution images from low resolution images, [5], for altering images so they resemble a particular painting or drawing, for skinning, [6], and for generating curves, [7]. By using an example, the user can often specify what kind of results should be produced more easily and more intuitively. Example-based techniques often apply more generally to a wider variety of models than other methods, [4]. For example, texture synthesis methods which use examples can generate a wider variety of textures than other methods such as Perlin noise, [8]. Even though example-based techniques have been applied to many areas of graphics, their use in modeling has been limited, [9].
In an example-based modeling technique, the user would provide a small example model and then the algorithm would generate a larger model that resembles it. This type of algorithm is called a model synthesis algorithm because it is similar to texture synthesis. Designing this type of algorithm for three-dimensional models is the central goal of this work.
In this paper, we address the problem of generating complex models using model synthesis. Model synthesis is a simple technique,[10-12], to automatically generate complex shapes. The model synthesis algorithm accepts a simple three-dimensional shape as an input and then generates a larger and more complex model that resembles the input.
Different procedural modeling techniques require varying degrees of user input. Using a high degree of user input has both advantages and disadvantages. Without sufficient user input, the result generated by the algorithm may be too random and some parts of the result may turn out to be different from what the user intended. With too much user input, the time required to adjust it could overwhelm the user. Ideally, the user could choose to provide any amount of input and the algorithm should be able to adjust accordingly. The user input can often be specified in the form of a constraint on the output. Any output that satisfies all of the users constraint is acceptable. Prior works in model synthesis [10-12] use a minimal amount of user input in the form of a single adjacency constraint and enabling the user to specify geometric constraints that give the user greater control over the results.
An important limitation in [10] is that the example models need to be manually decomposed into model pieces. This decomposition is not intuitive in most cases because all model pieces must have the same size and must occupy the space corresponding to every position in a three-dimensional lattice. In [11, 12] the example model is a set of polygons that form closed polyhedral objects. The amount of time and memory that model synthesis needs depends on the number of vertices and it considerably limits the complexity of the output model.
In this work, a novel model synthesis algorithm is presented which tries to generalize the previous approaches and solve part of the aforementioned limitations. With the aim of facilitating the example model design by the user, every three-dimensional object or shape, with independence of its size, is considered as model piece. Not only user constraints are considered but also example inherent constraints which are automatically generated based on geometric constraint solving, [13]. The existence of a certain distribution for the different model pieces on the surface or terrain on which the new model is built is another important issue taken into account. The objective is to obtain new models, more complex in output size (number of polygons and number of pieces), which exploit all the information (constraints, relationships among pieces) contained in an intuitively designed example model.
References
[1] B. Mandelbrot. The fractal geometry of nature. W. H. Freeman and Company, 1982.
[2] D.S. Ebert, F.K. Musgrave, D. Peachey, K. Perlin, and S. Worley. Texturing and Modeling: A Procedural Approach. Morgan Kaufmann Publishers, San Francisco, CA, 3rd edition, 2003.
[3] A.A. Efros and T.K. Leung. Texture synthesis by non-parametric sampling. In IEEE International Conference on Computer Vision, pages 1033-1038, Corfu, Greece, 1999.
[4] L.-Y. Wei, S. Lefebvre, V. Kwatra, and G. Turk. State of the art in example-based texture synthesis. In Eurographics 2009, State of the Art Report, EG-STAR. Eurographics Association, 2009.
[5] W.T. Freeman, T.R. Jones, and E.C. Pasztor. Example-based superresolution. IEEE Computer Graphics and Applications, 22(2):56{65, 2002.
[6] X. Shi, K. Zhou, Y. Tong, M. Desbrun, H. Bao, and B. Guo. Example-based dynamic skinning in real time. In SIGGRAPH '08: ACM SIGGRAPH 2008 papers, pages 1-8, New York, NY, USA, 2008. ACM.
[7] A. Hertzmann, N. Oliver, B. Curless, and S.M. Seitz. Curve analogies. In EGRW '02: Proceedings of the 13th Eurographics workshop on Rendering, pages 233-246, Aire-la-Ville, Switzerland, 2002. Eurographics Association.
[8] Ken Perlin. An image synthesizer. SIGGRAPH Comput. Graph., 19(3):287-296, 1985.
[9] Thomas Funkhouser, Michael Kazhdan, Philip Shilane, Patrick Min, William Kiefer, Ayellet Tal, Szymon Rusinkiewicz, and David Dobkin. Modeling by example. In SIGGRAPH '04: ACM SIGGRAPH 2004 Papers, pages 652{663, New York, NY, USA, 2004. ACM.
[10] P. Merrell. Example-based model synthesis. In I3D 07: Symposium on Interactive 3D graphics and games, pages 105-112. ACM Press, 2007.
[11] Paul Merrell and Dinesh Manocha. Continuous model synthesis. ACM Transaction on Graphics, 27(5):1-7, 2008.
[12] Paul Merrell and Dinesh Manocha. Constraint-based model synthesis. In SPM '09: 2009 SIAM/ACM Joint Conference on Geometric and Physical Modeling, pages 101-111, New York, NY, USA, 2009. ACM.
[13] R. Joan-Arinyo, A. Soto-Riera, S. Vila-Marta, and J. Vilaplana. On the domain of constructive geometric constraint solving techniques. In R. Duricovic and S. Czanner, editors, Spring Conference on Computer Graphics, pages 49{54, Budmerice, Slovakia, April 25-28 2001. IEEE Computer Society, Los Alamitos, CA.

