Construcción del concepto de número
Es conocido el experimento de Piaget relativo a la conservación de la cantidad discreta. Se presenta a un niño pequeño dos conjuntos de igual cantidad de objetos de la misma clase, dispuestos en filas simétricas, de forma que estén en correspondencia de uno a uno fácilmente perceptible de modo visual, como sugiere el siguiente dibujo:
0-0-0-0-0-0
Si se pregunta al niño en que fila hay más objetos, responde que en los dos iguales. Pero si se alejan entre sí los elementos de una de las dos filas,
0-0-0-0-0-0
0 - 0 - 0 - 0 - 0 - 0
muchos niños de Educación Infantil e, incluso, de primeros niveles de Primaria contestan que hay más elementos en la fila donde los objetos se han separado más. Incluso si aciertan con pequeñas cantidades, se equivocan al evaluar cantidades grandes.
Piaget dedicó gran atención a este problema, que definió como problema de conservación de la cantidad discreta. Para Piaget la construcción del concepto de número exige la previa posesión de diferentes capacidades lógicas, como son las capacidades de clasificar, de ordenar y de efectuar correspondencias, capacidades lógicas que -dentro de su teoría de evolución del pensamiento en forma de estadios- se alcanzan en el estadio de pensamiento operacional (operaciones concretas). De forma que sin la previa posesión de dichas capacidades, técnicas tradicionales de enseñanza del número natural, como la de contar, pueden reducirse a un mero procedimiento memorístico, sin mayor valor educativo.
El concepto de número natural se elabora muy lentamente. Comienza con una percepción global de la cantidad, expresada con términos tales como "muchos", "pocos", "algunos", "ninguno", etc. Continúa con comparaciones expresadas mediante términos como "más que", "menos que", "igual que". Un paso importante es el de simbolización del número, primero para pequeñas cantidades y luego para cantidades elevadas, sin ayuda de la percepción, que obliga a usar un sistema de numeración. El aprendizaje del sistema de numeración decimal no se completa hasta que no se alcanza un buen desarrollo de las estructucturas aditiva y multiplicativa.
Desde este punto de vista, el aprendizaje de los números naturales en Educación Infantil y Primer Ciclo de Primaria debería ir precedido y acompañado de actividades orientadas al desarrollo de capacidades lógicas, como las de clasificar, ordenar y de efectuar correspondencias. Por ejemplo, actividades con los bloques lógicos, que es un material didáctico específicamente diseñado para ese objetivo, compuesto por una variedad de figuras geométricas de diversos tamaños, colores y grosores, tales como las que aparecen en la figura siguiente.

Esta interpretación de Piaget es consecuente con la definición conjuntista del número natural. En primer lugar como cardinal, como propiedad en común de conjuntos coordinables entre sí, independiente de la naturaleza, forma, color, etc., de sus correspondientes elementos. En segundo lugar, como ordinal, ligado a la inclusión de clases, que permite comparar y ordenar los conjutnos por tamaño y, en consecuencia, discriminar los números entre sí.
Un punto de vista alternativo al de Piaget es el de psicólogos como Gelman y Gallistel o Baroody, quienes defienden la enseñanza de los números basada en la acción de contar, afirmando que las dificultades de los niños con la conservación de la cantidad es el resultado de un conocimiento incompleto de cómo se debe contar y no de una incapacidad para pensar lógicamente.
Para Steffe, en esa misma línea de pensamiento, contar como actividad es una coordinación de dos actividades productivas: la producción de una secuencia de palabras números y la producción de una secuencia de elementos contables.
De acuerdo con Steffe, el esquema conceptual inicial correspondiente a la actividad de contar podría ser el siguiente
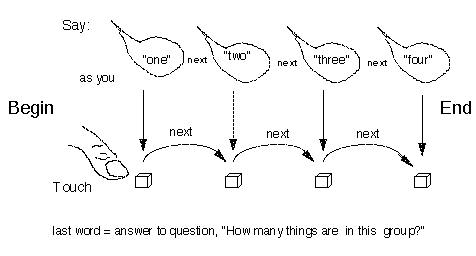
Para Piaget, el desarrollo lógico precede al desarrollo del pensamiento numérico. Pero para autores como Nesher, P., J. J. Greeno, et al., el conocimiento aritmético es uno de los mecanismos que facilita al niño la comprensión de las relaciones entre conjuntos y desempeña una función para construir las relaciones de clase, incluyendo la inclusión de clases.
La realidad es que los niños están inmersos en una cultura que basa la capacidad para cuantificar en la acción de contar. La realidad es que, una vez que se aprende la secuencia de palabras-números, la determinación del número de elementos de cualquier conjunto es muy fácil, apareciendo dicho número expresado mediante la última palabra-número de la secuencia. Esa inmersión cultural, inevitable hoy por hoy, da más sentido aún a las investigaciones que, sin cuestionar la importancia del desarrollo lógico sobre el desarrollo del pensamiento aritmético, fundamentan el aprendizaje numérico en las actividades de contar.
El desarrollo de la capacidad de contar sigue varias etapas, según Steffe et al. (1983, 88):
Etapa 0. Preperceptual. Cuando intentan contar, los niños son incapaces de coordinar las palabras números con los elementos que se cuentan.
Etapa 1. Perceptual. Los niños se limitan a contar aquellos elementos que pueden percibir, por ejemplo, ver.
Etapa 2. Figurativa. Los niños cuentan desde uno cuando resuelven problemas de adición con colecciones seleccionadas. Parecen visualizar los elementos y todos los movimientos son importantes (a menudo tipificados pasando la mano sobre objetos escondidos). Si tienen que contar dos colecciones de seis y de tres deben primero contar los seis elementos para comprender el significado de "seis", después contar los tres elementos, después contar la colección entera de seis y de tres.
Etapa 3. Secuencia numérica inicial. Los niños cuentan para resolver problemas de adición y de sumando desconocido con colecciones seleccionadas. Los niños no cuentan desde uno sino que comienza en el número apropiado. Si suman dos colecciones de seis y de tres entonces cuentan: seis, siete, ocho y nueve.
Etapa 4. Sucesión numérica implícitamente anidada. Los niños son capaces de centrarse en elementos unidad abstractos. Pueden contar hacia adelante y hacia atrás, escoger la más apropiada para resolver los problemas. Generalmente cuenta hacia atrás para resolver los problemas de sustracción.
Etapa 5. Sucesión numérica explícitamente anidada. Los niños controlan simultaneamente dos sucesiones numéricas y pueden desempotrar las unidades compuestas más pequeñas de la unidad compuesta que los contiene, y entonces compararlas. Esto es, pueden conceptualizar un total (por ejemplo 12), una parte (por ejemplo, 9) y el resto (por ejemplo, 3) simultaneamente. Comprenden que la adición y la sustracción son operaciones inversas.
De acuerdo con Case (1998), la construcción del concepto de número natural se efectúa sobre la base de determinados esquemas conceptuales, que se integran en otros más amplios propios del campo numérico. La idea de recta, de cuerda numérica es esencial en esos esquemas.
En una línea cercana, para Fuson y Hall, los niños acceden al dominio de la secuencia numérica en varios niveless:
* Nivel de cuerda: la sucesión comienza en uno, pero los términos parecen estar unidos (uno, dostres, cuatrocinco,...)
* Nivel de cadena irrompible: la sucesión comienza desde uno y los términos están diferenciados. Es el caso más común.
* Nivel de cadena rompible: a diferencia del anterior, la sucesión puede comenzar as partir de cualquiera de sus términos, aunque en sentido ascendente.
* Nivel de cadena numerable: la sucesión se utiliza en procesos en los que se comienza por un término cualquiera, contando n a partir de él para dar otro término por respuesta (cuatro, cinco, seis, siete, ocho).
* Nivel de cadena bidireccional: la sucesión puede recorrerse indistintamente en sentido ascendente o descendente, comenzando por un término cualquiera.
Puede apreciarse que la actividad de contar está estrechamente ligada a las operaciones de adición y substracción. En realidad, el aprendizaje de los números naturales es sobre todo el aprendizaje de la estructura del conjunto de los números naturales, que contiene las diferentes operaciones con los números, la adición y la substracción en particular. Pues conocer el número nueve implica conocer que es mayor que el ocho (ocho más uno); que es mayor que siete (siete más dos) ; que es menor que once (once menos dos); que es el doble de cuatro (es decir, cuatro más cuatro), etc.
Las operaciones suma y resta
El análisis de los problemas de adición y sustracción ha permitido identificar tres categorías fenomenológicas básicas : Cambio (une y separa), Combinación, y Comparación. En la Tabla I se da una descripción general de cada una de estas categorías, junto con ejemplos y títulos previos usados en el pasado para las mismas categorías.
|
Nombre actual de la Categoría |
Características
|
Ejemplo
|
Investigación y títulos previos para la misma Categoría |
| Combinación | Implica relación estática entre conjuntos. Pregunta por el conjunto Unión o por uno de los dos subconjuntos disjuntos | Hay 3 chicos y 4 chicas. ¿Cuántos niños hay en total? |
COMBINACIÓN: Greeno (1980a, b), Heller & Greeno (1978); Riley (1979), Riley Et al. (1981). PARTE-PARTE-TODO: Carpenter y Moser (1981),Carpenter et al. (1981). ESTÁTICA: Nesher (1978, 1981) COMPOSICION DE DOS MEDIDAS: Vergnaud & Durand (1976), Vergnaud (1981).
|
| Cambio | Describe el aumento o la disminución en algún estado inicial para producir un estado final | Juan tiene 6 cromos. Perdió 2 de ellos. ¿Cuántos cromos tiene ahora? |
CAMBIO: Greeno (1980a, b) UNIÓN Y SEPARACIÓN: Carpenter & Moser (1981) Carpenter et al. (1981). DINÁMICA: Nesher & Katriel (1978), Nesher (1981) TRANSFORMACION RELACIONANDO DOS MEDIDAS: Vergnaud & Durand (1976), Vergnaud (1981). |
| Comparación | Implica comparación estática entre dos conjuntos. Pregunta acerca del conjunto Diferencia o acerca de uno de los conjuntos sobre los que actúa el conjunto Diferencia. | Tom tiene 6 cromos. Joe tiene 4 cromos.¿Cuántos cromos tiene Tom más que Joe? |
COMBINACIÓN: Greeno (1980a, b), Carpenter & Moser (1981), Carpenter et al. (1981), Nesher & Katriel(1978) Nesher (1981) UNA RELACIÓN ESTÁTICA CONECTANDO DOS MEDIDAS: Vergnaud & Durand (1976), Vergnaud (1981) |
Para un estudio sobre los grados de dificultad de estas categorías puede consultarse http://copsa.cop.es/congresoiberoa/base/educati/a17.htm
Multiplicación y división
Determinados estudios señalan que los niños no siempre construyen
la multiplicación y algunos, simplemente no llegan a construirla (Orozco,
1996). Schlieman (1997) señala que los vendedores de dulces no utilizan
la multiplicación para resolver tareas de compra-venta de dulces. De
acuerdo con Resnick, los únicos conceptos fáciles de adquirir
y que parece se adquieren universalmente, son los basados en la composición
aditiva. (Resnick, 1986, p. 189).
Piaget (1983, 1987) señala que la multiplicación no se puede entender como una manera rápida de sumar repetidamente, sino que es una operación que requiere pensamiento de alto orden, que el niño construye a partir de su habilidad para pensar aditivamente. En esta medida, describe la diferencia entre la multiplicación y la adición en términos de la diferencia en los niveles de abstracción y del número de relaciones de inclusión que un niño puede realizar simultáneamente.
El pensamiento aditivo solamente involucra un primer nivel de abstracción, en el cual, cada unidad que el niño suma está hecha de unos que le exige establecer relaciones de inclusión en un primer nivel: los grupos se combinan sucesivamente. En contraste, la multiplicación involucra dos tipos de relaciones que no son necesarias para la adición: la correspondencia múltiple y la composición de relaciones de inclusión de más de un nivel. En el caso de 3 veces 5, por ejemplo, el niño debe convertir 5 unidades de uno en una unidad de 5; por supuesto, esto exige una abstracción superior a la requerida para pensar en unidades de uno. Ahora bien, al nivel de las unidades de 5 el niño debe contabilizar tres unidades de cinco. En la multiplicación, estas relaciones sucesivas de inclusión se deben dar simultáneamente.
Desde una perspectiva de procesamiento, Anghileri (1989) señala que la adición repetida es un procedimiento más complejo que la suma de dos numerales porque los niños tienen que manejar un patrón interno y guardar cada total. Así, los niños deben utilizar el segundo factor para terminar la reiteración del patrón que el niño utiliza en un punto determinado. En este mismo sentido, la coordinación de la cota y la operación de reiteración es lo que permite la transformación de las estrategias aditivas en multiplicativas. (Orozco, 1996).
Vergnaud (1983, 1988) analiza los problemas pertenecientes al campo conceptual de las estructuras multiplicativas desde la doble perspectiva de sus características matemáticas y las propiedades que resultan más "naturales" a los estudiantes. De acuerdo con este autor, los problemas multiplicativos pueden ser de tres tipos: de proporción simple, de producto de medida y de proporción múltiple.
Los problemas de proporción simple, donde hay que reiterar una cantidad un número de veces, son los más sencillos y admiten la posibilidad de una resolución exitosa procediendo sobre estrategias aditivas. Los de producto de medida, en los que dos magnitudes se componen para dar una tercera magnitud (por ejemplo, el cálculo de áreas), implican el establecimiento de coordinaciones entre dos dimensiones, por lo que podría considerarse que resultan más propiamente multiplicativos que los de proporción simple, al requerir necesariamente el seguimiento de estrategias multiplicativas para su resolución exitosa. Los problemas de proporción múltiple son los más complejos, en tanto involucran reglas de tres múltiples.
La investigación ha mostrado que, en general, frente a problemas multiplicativos, los niños tienden a utilizar estrategias o procedimientos aditivos y que este tipo de estrategia resulta suficiente para resolver correctamente algunos problemas multiplicativos. Esta tendencia persiste aún cuando ya han aprendido las tablas de multiplicar Vergnaud, 1983; Fischbein y cols., 1985; Gómez-Granell, 1987; Siegler, 1988; Anghileri, 1989; Mitchelmore y Mulligan, 1996; Orozco, 1996).
Las estrategias o procedimientos aditivos que los niños utilizan para solucionar problemas multiplicativos son la estrategia de enumeración o conteo, la de complemento y la de suma. Solo después los niños empiezan a utilizar estrategias propiamente multiplicativas.
Bibliografía
Anghileri, J. (1989). An investigation of young children’s understanding of
multiplication. Educational Studies in Mathematics, 20, 367-385.
Berh, M. J., Harel, G., Post, T., Lesh, R. (1991). Rational numbers: Toward a semantic analysis - emphasis on the operator construct. In T. Carpenter & E. Fennema (Eds.), Learning, Teaching and Assessing Rational Number Concept: Multiple Research Perspectives. Hillsdale, NJ: Erlbaum.
Campbell, J.I.D. & Clark, J.M. (1992). Cognitive number processing: an encoding complex perspective. In J.J.D. Campbell (Ed.), The Nature and Origins of Mathematical Skill.
Carraher, T. N. (1986). From drawings to buildings; working with mathematical
scales. International Journal of
Behavioral Development, 9, 527-544.
Davydov, V. V. 1982. The psychological characteristics of the formation of elementary mathematical opertion in children. In Addition and subtraction: A Cognitive perspective, ed. T.P. Carpenter, J. Moser, and T. A. Romberg. Hillsdale, NJ: Lawerence Erlbaum Associates.
Dehaene, S. (1992). Varieties of numerical abilities. Cognition, 44, 1-42.
Fischbein, R., Deri, M., Nello, M., y Marino, M. (1985). The Rol of Implicit
Models in Solving Verbal Problems in
Multiplication and Division. Journal for Research in Mathematics Education,
16, 3-17.
Freudenthal, H. 1983. Didactical phenomenology of mathematical strucrtures, 133-209. Boston: D. Reidel
Fuentes Loss, M. (1996). La comprensión y producción de numerales
en niños sordos. Barcelona: Tesis Doctoral,
Departamento de Psicología Evolutiva y de la Educación, Facultad
de Psicología, Universidad de
Barcelona.
Galperin, P. Y., and L.S. Georgiev. 1969. The formation of elementary mathematical notions. In Soviets studies in the psychological of learning and teaching mathematics, ed. J. Kilpatricks and I. Wirszup.
Gómez-Granell, C. (1987). Representación y simbolización
en el marco de problemas multiplicativos. Barcelona:
Tesis doctoral no publicada. Universidad de Barcelona.
Hiebert, J., and D. Wearne. 1992. Links between teaching and learning place value with understanding in firts grade. Journal for Research in Mathematics Education. 23(2): 98-122.
Kamii, C. (1986). Place Value: An explanation of its difficulty and implications
for the primary grades. Journal for
Research in Childhood Education, 1,. 75-86.
Kamii, C. (1992). Reinventando la aritmética II. Madrid: Aprendizaje-Visor.
Lee, K. y Karmiloff-Smith, A. (1996). The Development of External Symbol
Systems: The Child as a Notator. En: Gelman, R. & Kit-Fong Au, T. (Eds.)
Perceptual and Cognitive Development. San Diego: Academic Press, 185-241
Lerner, D. y Sadovsky, P. (1994). El sistema de numeración: un problema
didáctico. En Parra, C. y Saiz, J. (comp.), Didáctica de las
matemáticas. Buenos Aires, Paidós, 95-184.
Martínez-Ruiz, S. (1995). Análisis evolutivo del principio de valor posicional en situaciones de producción, interpretación y uso de numerales. Barcelona: (Tesis Doctoral) Departamento de Psicología Evolutiva y de la Educación, Facultad de Psicología, Universidad de Barcelona.
McCloskey, M., (1992). Cognitive mechanisms in numerical processing: Evidence from acquired dyscalculia. Cognition, 44, 107-157.
McCloskey, M., Aliminosa, D., y Sokol, S. (1991). Facts, rules and procedures in normal calculation: Evidence from multiple single-patient studies of impaired arithmetic fact retrieval. Brain and Cognition, 17, 154-203.
McCloskey, M., Caramazza, A. (1985). Cognitive Mechanisms in Number Processing
and Calculation: Evidence
from Dyscalculia. Brain and Cognition, 4, 171-196.
Mitchelmore, M., Mulligan, J. (1996). Children’s developing multiplication and division strategies. In L. Puig, A. Gutiérrez (Eds.). Proceedings of the 20th Conference of the International Group for the Psychology of Mathematics Education. Vol. 3. Valencia (Spain): Universitat de València. Dept. de Didàctica de la Matemàtica, 407-414.
Orozco, M. (1996). Estudio microgenético y procesual de la construcción de la operación multiplicativa. Barcelona: Tesis Doctoral, Departamento de Psicología Evolutiva y de la Educación, Facultad de Psicología, Universidad de Barcelona.
Orozco, M. y Hederich, C. (2000). Errores de los niños al escribir numerales dictados. (En prensa).
Piaget, J. (1987). Possibility and Necessity. Minneapolis: University of Minnesota Press. (Trabajo Original Publicado en 1983).
Pontecorvo, C. (1996). La notación y el razonamiento con números
y nombres en el período preescolar y en la
escuela primaria. Infancia y Aprendizaje, 74, 3-24
Resnick, L. (1983). A development theory of number understanding. En H. P. Ginsburg (Ed.), The development of mathematical thinking. Nueva York: Academic Press, 110-151.
Resnick, L. B. (1986). The development of mathematical intuition. In M.. Perlmutter (Ed.), Perspectives on Intellectual Development. Minnesota Symposia on Child Psychology, 9, 159-194.
Scheuer, N., Sinclair, A., Merlo de Rivas, S. y Tièche, C.. (2000) Cuando ciento setenta y uno se escribe 10071: niños de 5 a 8 años produciendo numerales. Infancia y Aprendizaje, 90, 31-50.
Schliemann, A. D. (1997). Razonamiento lógico-matemático en
contextos socioculturales. Dossier-Debate Revista
Colombiana de Psicología, 5-6, 11-19.
Siegler, R. S. (1988). Strategy choice procedures and the development of multiplication skills. Journal of experimental Psychology General, 117, 258-275.
Sinclair, A. (1988). La notation numérique chez l’enfant. En H. Sinclair
(comp). La production de notations chez
le jeune enfant: langage, nombre, rytmes et mélodies. Paris: PUF, 71-98.
Tolchinsky, L., Karmiloff-Smith, A. (1991). Las restricciones del conocimiento
notacional. Psicología Educativa,
16-17, 39-90.
Vergnaud, G. (1983). Multiplicative structures. In R. Lesh and M. Landau (Eds.), Acquisition of Mathematics: Concepts and Processes. New York: Academic Press, 128-174.
Vergnaud, G. (1988). Multiplicative structures. In J. Hiebert, J. and M. Behr. Number Concepts and Operations in the Middle Grades. Vol 2. Reston, Virginia: The National Council of Teachers of Mathematics, Inc., Second Printing 1989, 141-161.