Hace algunos años el físico Lucien Hardy propuso un experimento imaginario y una paradoja dentro de la Física Cuántica. De acuerdo con la interpretación de Copenhage de la Física Cuántica, cuando realizamos una medida de un sistema físico se produce un cambio en el estado del sistema (reducción o colapso del paquete de ondas). Este cambio no se refiere a un cambio sobre nuestra percepción del sistema sino a un cambio real sufrido por el sistema. Por otro lado, la única forma que tenemos de conocer un sistema es midiendo sobre él y por tanto produciendo dicho colapso en el estado del sistema.

Hardy propone que puesto que nosotros no podemos influir sobre el pasado, al no poderlo modificar, no tiene sentido hablar del pasado ya que no podemos conocerlo puesto que de acuerdo con la teoría cuántica conocer implica cambiar, modificar.

Pues bien, los físicos Aephraim Steinberg y Jeff Lundeen de la Universidad de Toronto han construido un dispositivo experimental en el que se realiza una "medida débil", basándose en la teoría desarrollada por  Yakir Aharonov de la Universidad de Tel Aviv. Mediante esta medida débil, se obtiene información sobre el sistema produciendo una perturbación en el sistema menor que la indeterminación de la magnitud que se quiere medir. De este modo la medida provoca un cambio en el sistema que es imperceptible desde el punto de vista del sistema. Este tipo de medida podría resolver la paradoja de Hardy.

Voy a analizar a continuación el experimento de Hardy. Supongamos que tenemos un par de interferómetros de Mach-Zehnder: uno para positrones y otro para electrones, como se muestra en la figura. El interferómetro consiste en una fuente de partículas (de positrones o electrones en nuestro caso), dos divisores de haz (splitters), dos espejos y dos detectores. Vamos a suponer que tal como se muestra en la figura los dos interferómetros están separados. Analicemos por separado cada interferómetro.

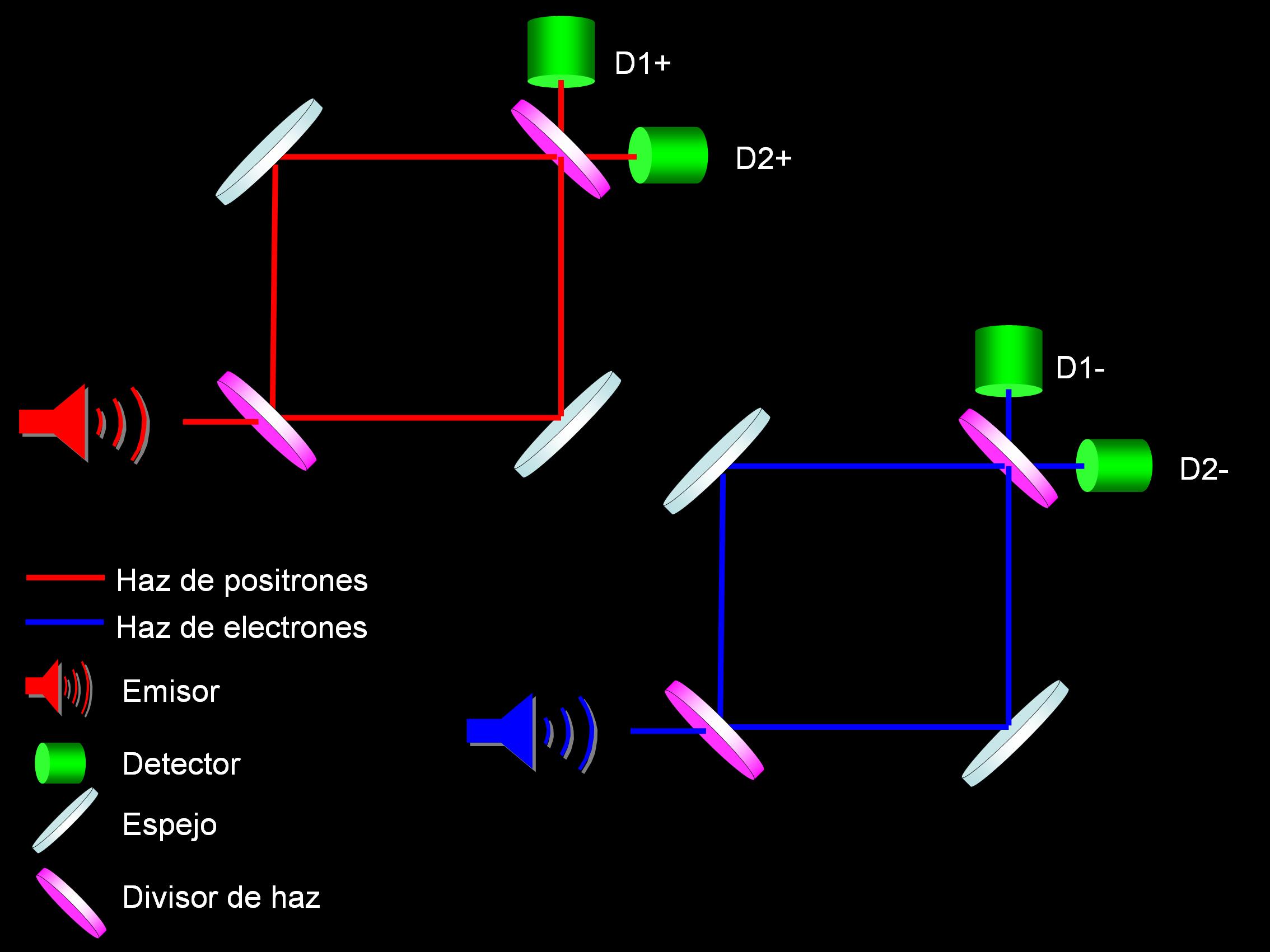En el caso del interferómetro para positrones, lo que llega a cada detector D1+ y D2+ es la interferencia de los haces que han recorrido los dos caminos producidos por el primer divisor. Vamos a suponer que los recorridos de los brazos del interferómetro son tal que la interferencia sea constructiva en el haz final que va a parar al detector D1+ y destructiva para el D2+, de modo que solamente el detector D1+ recibe positrones. Cualquier cambio que realicemos en el interferómetro, bien cambiando las dimensiones de los brazos o bien introduciendo un obstáculo en uno de los brazos, producirá que el detector D2+ también reciba positrones.

Por otro lado, supondremos que el interferómetro de electrones tiene las mismas condiciones, de modo que la interferencia que se produce en el detector D1- es positiva y la del D2- negativa. Por tanto, sólo el detector D1- recibe electrones. Cualquier modificación sobre las condiciones del interferómetro producirá que el detector D2- también reciba electrones.

Vamos a suponer ahora que colocamos los dos interferómetros tal como se muestra en la siguiente figura, de modo que haya una región en la que dos subhaces de positrones y electrones se cruzan, se solapan.

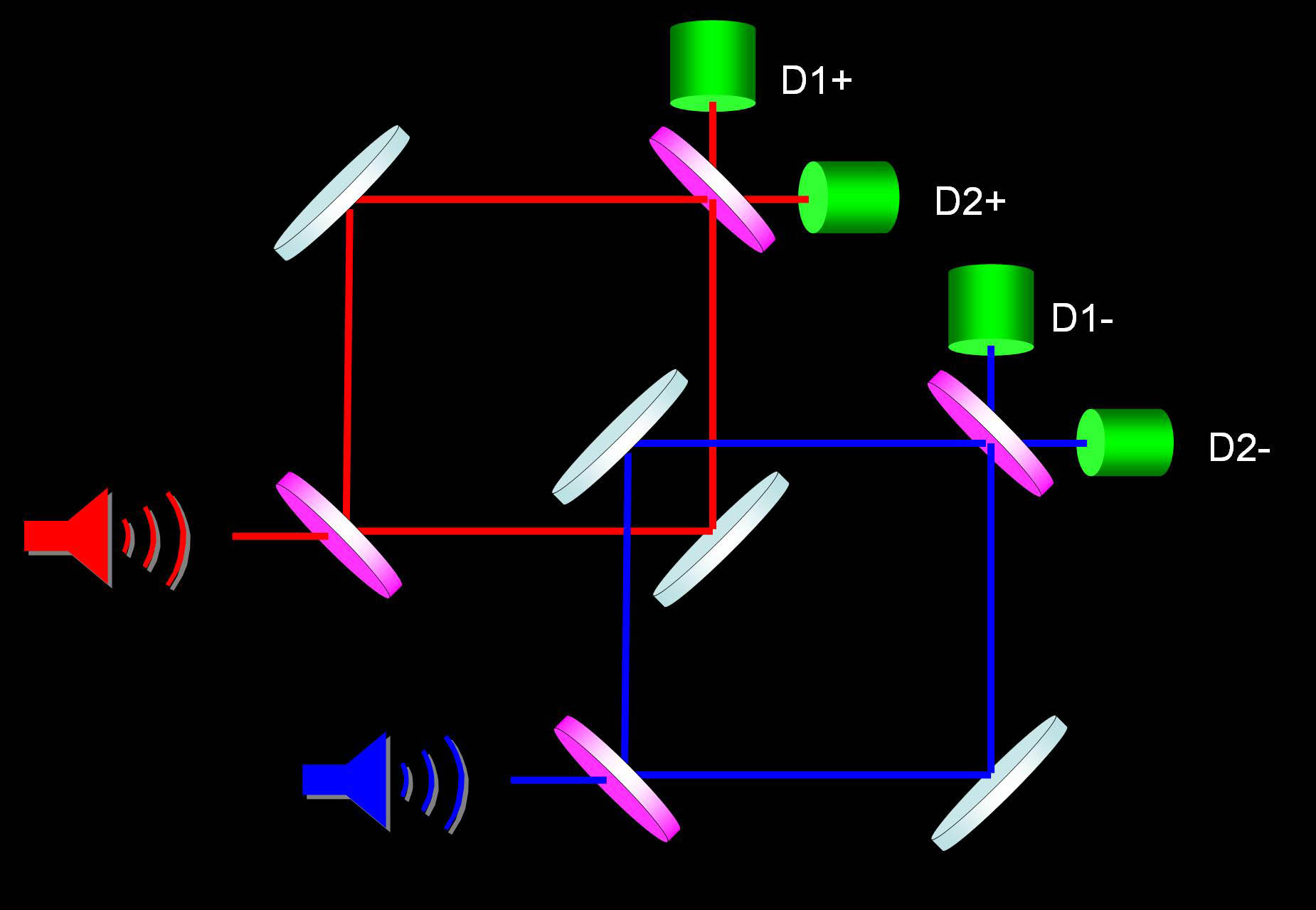
Como hemos modificado las condiciones de los interferómetros, se puede comprobar que ahora hay cierta probabilidad de que los detectores D2+ y D2- reciban partículas. Sin embargo existe una contradicción si pensamos desde el punto de vista clásico y tenemos en cuenta que si un positrón y un electrón se cruzan se aniquilan. Supongamos que los detectores D2+ y D2- reciben partículas tal como predice la teoría. Esto quiere decir que las partículas han notado algún cambio respecto del caso en el que los interferómetros estaban separados. Pero como el cambio consiste en que ahora hay una región de solapamiento entre los haces de positrones y electrones quiere decir que los electrones y positrones han tenido que pasar obligatoriamente por esa región de solapamiento. Pero si han pasado por esa región se han aniquilado y por tanto no deberían llegar a los detectores puesto que no existen. Llegamos inevitablemente a una contradicción.

Podemos ahondar un poco más desde otro punto de vista. Si llegan electrones al detector D2- podemos deducir que los positrones han recorrido la región de solapamiento, ya que si no los electrones no hubieran notado ningún cambio respecto del caso en el que los interferómetros estaban separados (en cuyo caso acabarían en el detector D1-). Por otro lado, como no ha  habido aniquilación ya que las partículas llegan a los detectores, podemos deducir que los electrones también han tenido que recorrer la región de solapamiento, ya que si no los positrones no llegarían al detector D2+ (ya que de nuevo no notarían ningún cambio respecto del caso en el que los interferómetros estaban separados). Por tanto llegamos de nuevo a una contradicción, ya que si tanto los electrones como los positrones han recorrido la región de solapamiento inevitablemente se han aniquilado y no pueden llegar a los detectores.

Podríamos intentar ver qué ocurre experimentalmente colocando un detector, por ejemplo, en el haz de electrones que se dirige hacia la región de solapamiento y antes de que lleguen a dicha región. Si este detector detecta un electrón quiere decir que éste atravesará la región de solapamiento. Pero en este caso, como estamos introduciendo un cambio en el interferómetro de los electrones, podrán llegar electrones hasta el detector D2-, aún en el caso de que no haya positrones. Por tanto, este detector no nos permite resolver la paradoja ya que no nos permite medir qué ocurre. Esto quiere decir que no existe paradoja alguna desde el punto de vista experimental ya que cuando realizamos un experimento que nos permita saber lo qué ocurre (pongamos donde pongamos los detectores que nos permitan saber el camino que recorrió cada partícula), el experimento no es resolutivo.

De acuerdo con la teoría propuesta por Yakir Aharonov se pueden realizar medidas débiles que produzcan una mínima perturbación en el sistema, lo que podría resolver la paradoja. Steinberg y Lundeen han conseguido por primera vez realizar estas medidas débiles, que nos permitirían resolver la paradoja del experimento de Hardy y HABLAR DEL PASADO!!!

Otro día analizaré en qué consisten las medidas débiles propuestas por Aharonov.

Enlaces

• El artículo de Aharonov se puede consultar online y es muy interesante.
• Artículo de Scientific Blogging.
• Artículo de Science Daily.